Gas Dynamics &
|
Two-Dimensional Compressible FlowPreviously only one-dimensional flows have been considered. While it is difficult to find a true one-dimensional flow in nature, 1-D analysis allows explanation of the various concepts and general calculations to be done. Using the 1-D concepts it is possible to extend the analysis to two-dimensional flows, in particular supersonic flows. Main features of interest are
Oblique Shock WavesNormal Shocks occur in one-dimensional flow. Normal Shocks occur in ducts and pipes, but for many flows only Oblique Shocks are encountered. These are not normal to the flow - shocks formed at the nose of wedge when a supersonic flow flows past, the shock in front of a body in a supersonic flow. Examples of these have been sketched in Fig. 26. 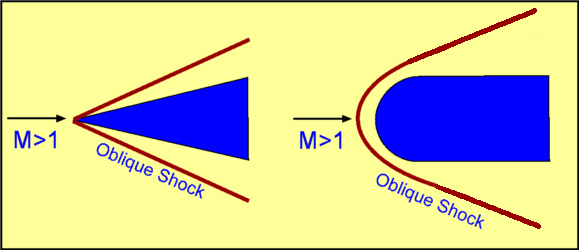 Figure 26 : Examples of Oblique Shock. 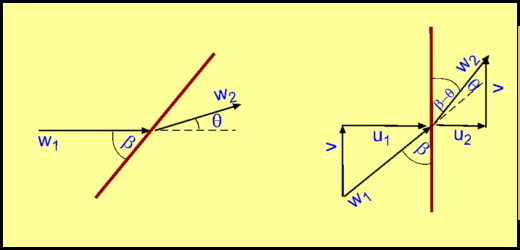 Figure 27 : Velocity Components for an Oblique Shock. Consider an oblique shock as shown in Fig. 27. Looking at the velocity components and comparing with that for a normal shock, it is clear that there is now an additional one, i.e, a tangential component, $v$ . Accounting for this is not a major problem. The shock mechanism is such that this component is unchanged across the oblique shock. However, the normal component $u_1$ does undergo a change as if it encountered a normal shock and comes out with a value $u_2$ on passing through the shock. For normal shocks $u_2<u_1$ . A close look at Fig. 27 reveals that the flow undergoes a turn as it passes through an oblique shock and the turn is towards the shock. Relations across an Oblique ShockThe angle $β$ between the shock and the incoming flow is called the Shock Angle. The angle through which the flow turns is $θ$, termed Deflection Angle. If $M_1$ is the incoming mach number then, $$β=\tan^{-1}(u_1/v)$$ Define, Oblique shock in Fig. 27 can be viewed as a normal shock with an incoming Mach Number equal to $M_1\sin(β)$, but with a tangential velocity component, $v$ superposed everywhere. Then it is a simple matter to calculate conditions across an oblique shock. In the normal shock relations, just replace Mach Number $M_1$ with $M_1\sin(β)$. Thus, It should be noted that $M_2\sin(β - θ)$ is the normal component of Mach Number downstream of the shock and is equal to, The other relations across the shock are given by, $$ρ_2/ρ_1=u_1/u_2={(γ+1)M_1^2\sin^2(β)}/{(γ-1)M_1^2\sin^2(β)+2}$$ $$T_2/T_1={(1+{γ-1}/2M_1^2\sin^2(β))({2γ}/{γ-1}M_1^2\sin^2(β)-1)}/{M_1^2\sin^2(β)({2γ}/{γ-1}+{γ-1}/2)}$$ $$P_{02}/P_{01}=({1/2(γ+1)M_1^2\sin^2(β)}/{1+1/2(γ-1)M_1^2\sin^2(β)})^{γ/{γ-1}}(1/{{2γ}/{γ+1}M_1^2\sin^2(β)-{γ-1}/{γ+1}})^{1/{γ-1}}$$ $${s_2-s_1}/R=1/{γ-1}\ln({2γM_1^2\sin^2(β)}/{γ-1}-{γ-1}/{γ+1})+γ/{γ-1}\ln({2+(γ-1)M_1^2\sin^2(β)}/{(γ+1)M_1^2\sin^2(β)})$$ The upstream flow for a normal shock must be supersonic, i.e., Thus for a given Mach Number, $M_1$, there is a minimum shock angle, which is given by ${\sin}^{-1}(1\/M_1)$, the maximum inclination is $π\/2$. Accordingly, the condition we have for an oblique shock is that, The lower limit $β={\sin}^{-1}(1\/M_1)$ gives a Mach Wave which gives a zero flow turn. The higher limit $β=π\/2$ gives a normal shock, which also gives a zero flow turn but perturbs the flow strongly. This gives the highest pressure jump across the shock. It should also be noted that the normal component of Mach Number downstream of the shock, $M_2 \sin(β - θ)$ must be less than $1$, i.e, must be subsonic. However when this normal component is combined with the tangential flow, the resulting magnitude of velocity behind the oblique shock is in most cases supersonic. Relation between β and θFor a given Mach Number $M_1$ a relationship between shock angle $β$ and flow deflection angle $θ$ can be derived. which gives leading to It is easily seen that $\tan(θ)$ has two zeros, one at $β={\sin}^{-1}(1\/M_1)$ and the other at $β=π\/2$. These correspond to the two limits we have on the shock angle $β$ The expression also has a maximum somewhere in between these two zeros. Fig. 28 shows the relationship between $θ$ and $β$. plotted for various Mach Numbers. For a given value of $θ$ we see that there are two values of $β$, indicating that two shock angles are possible for a given flow turning and an upstream Mach Number. For a given Mach Number there is a maximum flow turning, $θ_{max}$. 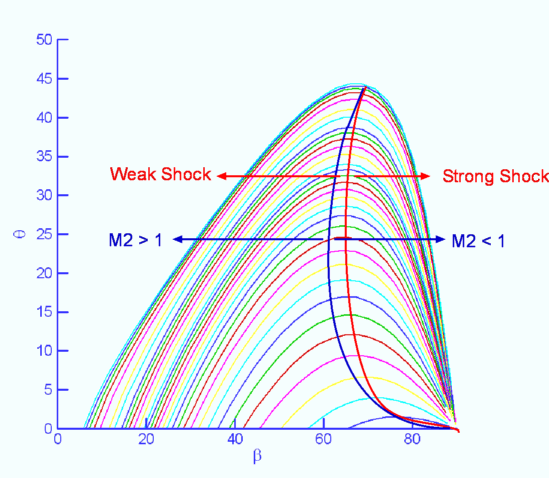 For $θ < θ_{max}$ , there are two values of $β$. The smaller value gives what is called a Weak Solution. The other solution is called a Strong Solution. The figure also shows the locus of solutions for which $M_2 = 1$. A strong solution always gives rise to a subsonic flow downstream of it, i.e, $M_2 < 1$ . The weak solution gives a supersonic flow downstream, except in a narrow band, with $θ$ slightly smaller than $θ_{max}$. Conditions across an oblique shock can be found in downloadable information, data sheets and scripts in the end of this section. Supersonic Flow past Concave Corners and WedgesThe following applications lead to weak solutions for the oblique shocks. For example, the flow past a concave corner and the flow past a wedge. 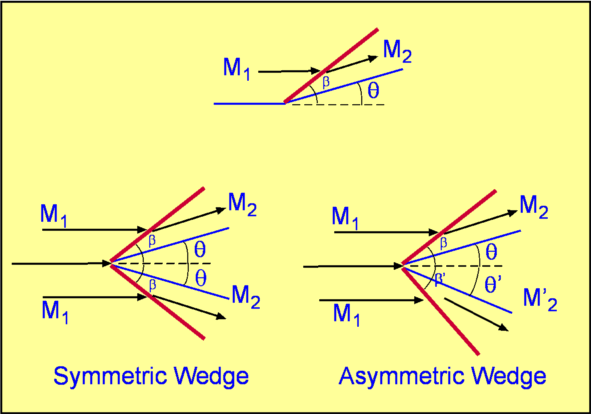 Figure 29 : Supersonic Flow past Concave Corners and Wedges A supersonic flow at Mach Number $M_1$ running past a concave corner inclined at an angle $β$ to the incoming flow is shown in Fig. 29. At the corner, the flow has to turn though an angle $θ$ because of the requirement that the normal component of velocity at any solid surface has to be zero. To facilitate this turn we require an oblique shock at an angle $β$ to form at the corner. The shock angle can be calculated for a given Mach Number and angle $θ$. The same theory can be applied in case of a symmetric or asymmetric wedge of half angle $θ$ as shown in Fig. 29. In both these cases the shocks are formed at the corner or the nose of the body. They are called Attached Shocks. As supersonic flows have limited upstream influence, then the flow on the lower surface of the wedge is independent of the flow on the upper surface. Weak Oblique ShocksFor small deflection angles it is possible to reduce the oblique shock relations to simple expressions. These are, The above expression indicates that the strength of the shock, denoted by the term $ΔP\/P$ is proportional to the deflection angle, $θ$. It can be shown that the change of entropy across the shock, $Δs$ is proportional to the cube of the deflection angle, Another useful expression for a weak oblique shock is for the change of speed across it, $${Δw}/w_1≈-θ/{√{M_1^2-1}$$ Supersonic Compression by TurningShock waves produce a mechanism to compress supersonic flow. If the flow is turned around a concave corner, an oblique shock is produced. As the flow passes through the shock its pressure increases. This lends itself to a simple method of compression. The effeciency of this method will depend on the shapes used to produce the compression. Firstly consider a compression through a single oblique shock. (Fig. 30). The flow turns through an angle $θ$, such that There is a loss of energy in this process. Entropy increases across the shock, the total pressure decreases, proportional to $θ^3$. 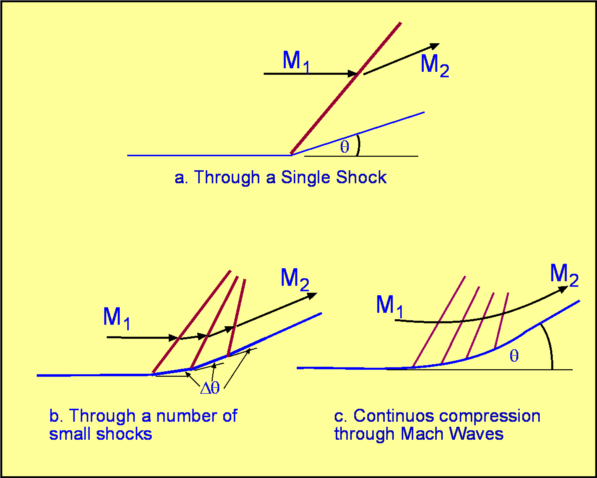 Figure 30 : Compression of a Supersonic Flow by Turning Secondly, consider compressing the flow through a number of shocks, say $n$ . Each shock is such that the flow downstream is supersonic. The flow turning angle through each of the shocks is $Δθ= θ\/n$. Consequently through n shocks, Change in pressure: $n {ΔP}\/n= ΔP$ Entropy rise: $n (θ\/n)^3 = θ^3\/n^2$ Thus, this arrangement gives the same compression as before, but the entropy rise is reduced enormously implying that losses are controlled. A limiting option is possible. If $n$ tends to $∞$. That is compression is effected by an infinite number of waves, i.e, Mach Waves. Instead of a concave corner there is now a smooth concave surface (Case (c) in Fig. 30). Now the compression is effected as before but the losses are zero because, The entire process is thus isentropic and the most efficient. Convergence of Mach Waves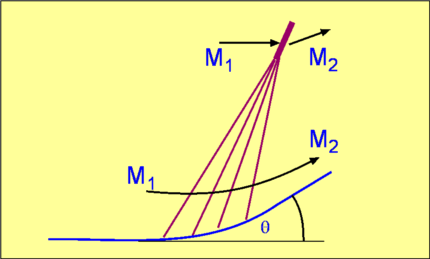 Figure 31 : Coalescence of Mach Waves to form an Oblique Shock. 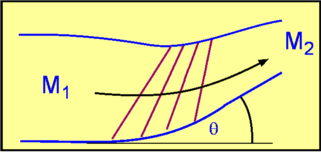 Figure 32 : Isentropic compression and expansion of a flow.
Figure 32 : Isentropic compression and expansion of a flow.
If the compression around a concave surface which takes place through a series of Mach Waves, then as the flow passes through each Mach Wave, pressure rises and the Mach Number decreases. Consequently, the wave angle $μ$ increases. This leads to a convergence of Mach Waves far from the concave surface as shown in Fig. 31. This phenomenon is called Coalescence . The waves merge and become an oblique shock. When this happens the flow is no longer isentropic, severe non-linearities build up. If an isentropic compression is required, then it is necessary that waves do not converge. This can be brought about by placing a wall forming a duct as shown in Fig. 32. |